Involutes of primitive 2D Shapes
So what is an Involute, if you took a string that was 300mm long and tied it to the bottom right hand vertex of an equilateral tringle (where each side is 100mm) and wrapped the string anti-clockwise around the triangle. Then pulled on the string hard and maintained it’s tension while unwrapping it clockwise its end vertex would scribe a spiral or in this case a triangular involute.
What’s interesting is as the string scribes an arc through the first 120degrees its radius to 100mm, through the next 120degress its radius is 200mm and finally the last 120degrees will have a radius of 300mm, at each transition the arcs are tangent.
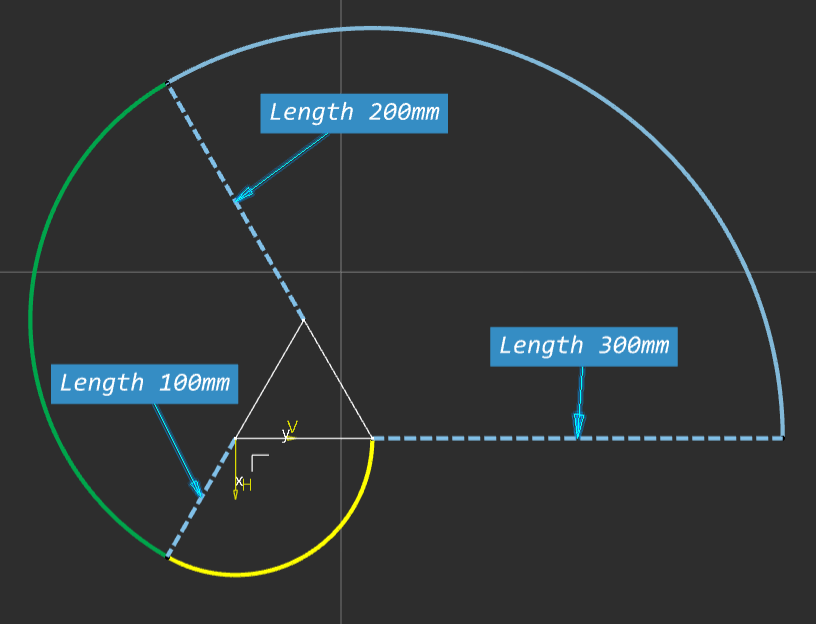
We can follow the same process for a square, this time each arc is scribed through 90degrees and four segments.
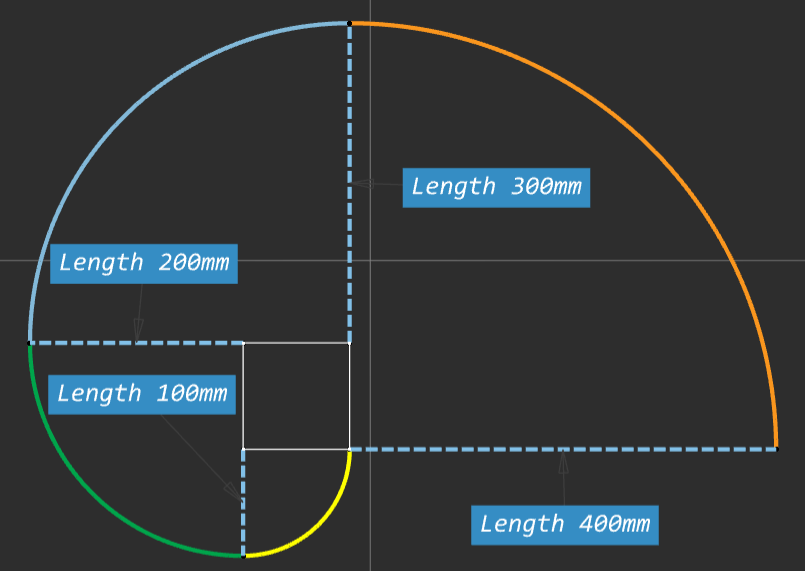
And the same process for a Hexagon, this time each arc is scribed through 72degrees and five segments.
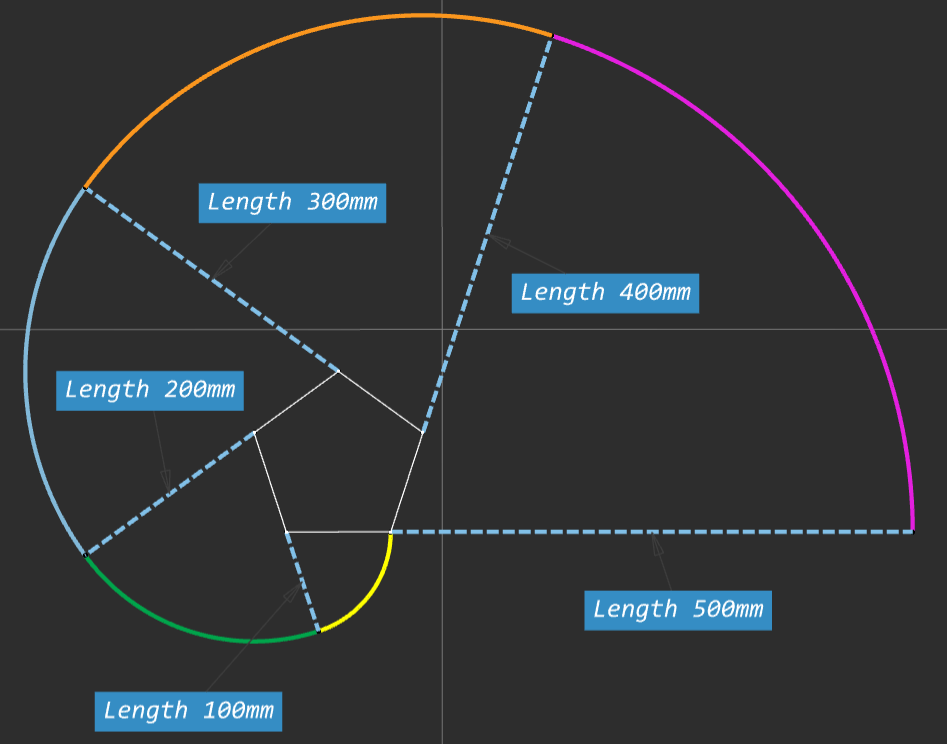
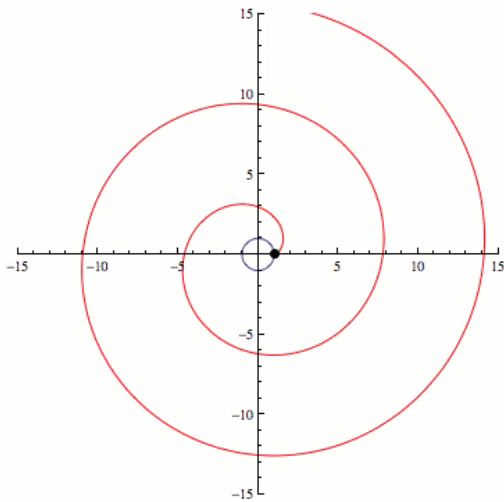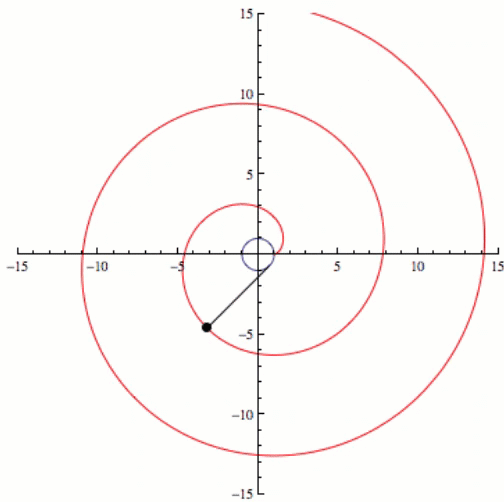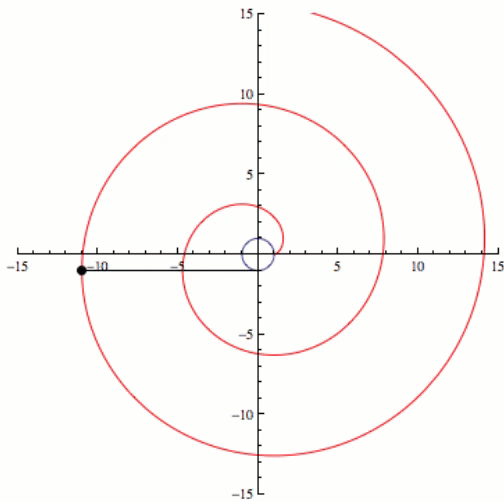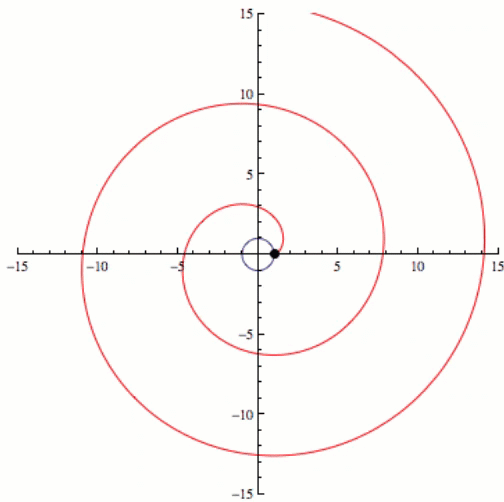
If we kept going and increasing the complexity eventually we would have an infinite number of sides or a circle, and the involute of a circle is a spiral. This can be seen in the video below.