Trigonometry Math Problem

Trigonometry Math Problem

My wife’s friend’s child was having a problem with a trigonometry math problem and wanted some help, It took me a while but i figured I would post the problem and the solution for fun.

The Problem

So we have a triangle and we need to find the angle in degree’s at D. We are given three of the angles A, B, C in terms of X.

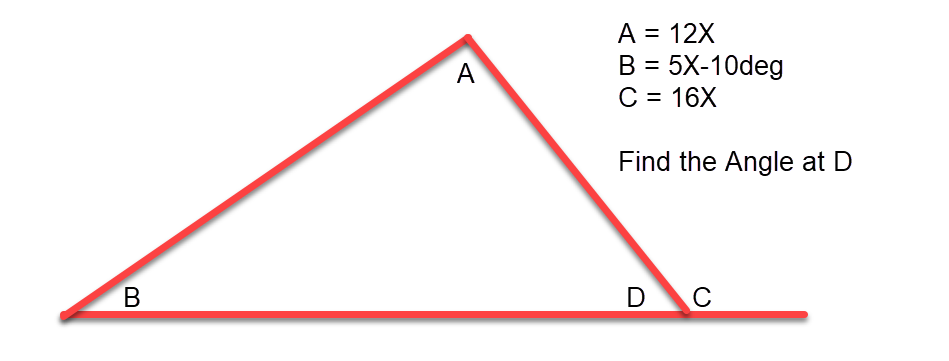
The Solution

To start the problem we have to make some assumptions;

1. We know that the sum of the angles in a triangle equals 180deg.
2. The Sum of angles D, and C must equal 180deg

Step 1 – Establish the Equation of a Triangle

If we know that the Sum of the angles in a triangle equals 180deg then we can write the following equation;

180\degree = A+B+D \\
180\degree = 12X+5X-10\degree+D \\
where \\
D=180\degree - 16X \\
so \\
180\degree = 12X+(5X-10\degree)+(180\degree - 16X) \\

Step 2 – Rearrange the Equation

So we have the equation for the triangle defined we now need to get it in terms of X = Value by rearranging the equation, so lets start.

Remember when moving a value from one side of the equals to the other its will change from being positive to negative or visa-versa.

180\degree = 12X+(5X-10\degree)+(180\degree - 16X) \\
 \text{Move the 180\degree to the other side of the equals.} \\
0 = 12X+(5X-10\degree)+(180\degree - 16X) -180\degree \\
\text{Let's now move the X terms to the Right-hand side of the equals symbol.} \\
-12X-5X+16X = -10\degree + 180\degree - 180\degree \\
\text{Let's sum up the values on either side of the equals symbol.} \\
-1X=-10\degree
\text{To make it simpler switch the two terms over to make them both positive.} \\
10\degree=1X \\ or \\X = 10\degree

Step 3 – Substitution

Now we know the value of X=10deg, we can now substitute back into our original four terms.

A = 12X = 12*10\degree = 120\degree \\
B = 5X-10\degree = (5*10\degree) -10\degree = 40\degree \\
C = 16X = 16*10\degree = 160\degree \\
D = 180\degree - C = 180\degree - (16X) = 180\degree-(16*10\degree) = 20\degree

Step 4 – Validation

Last step is to validate that the angles within the triangle summate to 180deg and that Angles C + D = 180deg, which were the two assumptions that we made at the start.

A+B+D = 120\degree + 40\degree + 20\degree = 180\degree \\
and \\
C + D = 160\degree+20\degree = 180\degree

We can quite clearly see that we have the correct values.

Job done.