Transformation Matrices – Direct 3D Rotations

Admin
Post Views: 267
Print Friendly, PDF & Email

Transformation Matrices – Direct 3D Rotations

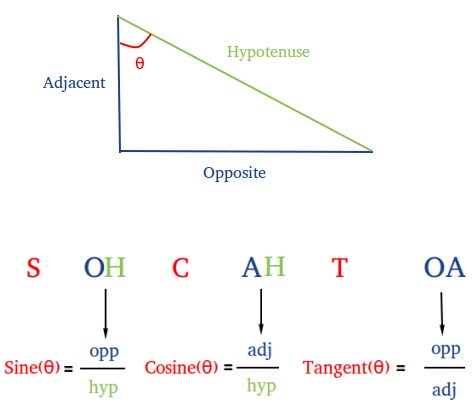
So again a big thank you to Catarina Carvalheiras, were going to take a look at rotations this time with no translations this means we have to go back to basics a little, ok a lot we all remember basic Trigonometry and how the three ratio rules help us analyze right angled triangles.

SOHCAHTOA
SOH-CAH-TOA

We can take this a step further, first we need to assume that Vector : V1 is a unit vector meaning it has magnitude or length of 1, and Vector : V2 is infinite. We can construct a right angled triangle by projecting V1 onto V2. So O : Opposite = Sinθ * H and A : Adjacent or the Projection = Cosθ * H.

Length of Vector Projection

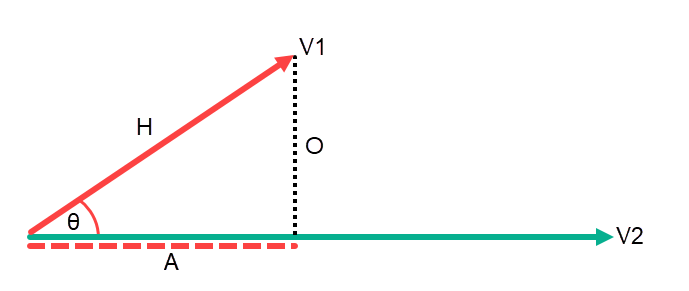
We can simplify these expressions since we know H is a Unit vector V1.

O = Sinθ \cdot H \\
O = Sinθ \cdot V1 \\
O = Sinθ \cdot 1 \\
\bold{O = Sinθ} \\
and \\
A = COSθ \cdot H \\
A = COSθ \cdot V1 \\
A = COSθ \cdot 1 \\
\bold{A = COSθ} \\

If we now take a frame of reference X0Y0 and rotate it about θ to create a second frame of reference X1Y1, we can create four right-angled triangles and four projections. We need to determine if each projection is either Sinθ or Cosθ.

2D Rotation Projections

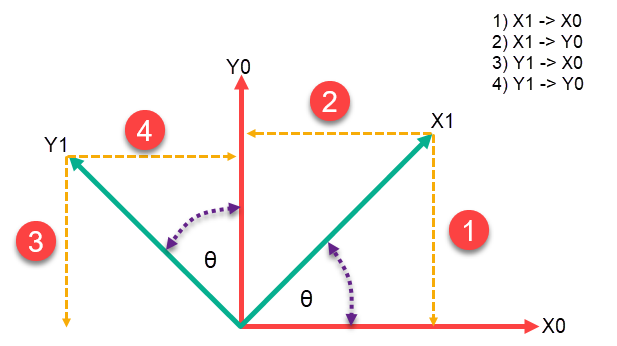
The first projection of X1 onto X0 is adjacent to our angle so its Cosθ which means our second projection has to be Sinθ, they are both projections onto the positive axes so they are both +. Projection Y1 onto -X0 (notice the negative) is opposite to our angle so it’s -Sinθ which means our fourth projection is Cosθ.

You should be able to see the pattern if projection 1 is Cos then projection 2 will be Sin, and if projection 3 is Sin then projection 4 will be Cos.

If the projection is projected onto an imaginary or negative axis then it will be negative, this is the case with projection 3.

so for the case above we can write this in mathematical form.

R {0 \atop 1} = 

\begin{bmatrix}
   \begin{bmatrix} 
       \underrightarrow{N_{X1}}
    \end{bmatrix}\\
   \begin{bmatrix} 
       \underrightarrow{N_{Y1}}
    \end{bmatrix}\\
\end{bmatrix} =

\begin{bmatrix}
   \begin{bmatrix} 
       \underrightarrow{X1XO}, & \underrightarrow{X1YO}
    \end{bmatrix}\\
   \begin{bmatrix} 
        \underrightarrow{Y1XO}, & \underrightarrow{Y1YO}
    \end{bmatrix}\\
\end{bmatrix} =

\begin{bmatrix}
   Adj, & Opp \\
   -Opp, & Adj
\end{bmatrix} =

\begin{bmatrix}
   Cosθ, & Sinθ \\
   -Sinθ, & Cosθ
\end{bmatrix}

Note: – In the translation only examples the vectors were written vertically, we can see with the rotation only the vectors are written horizontally.

For this example lets assume that θ = 90 and we know there are no translations.