EKL Sorting Lines in Respect to an AxisSystem

EKL Sorting Lines in Respect to an AxisSystem

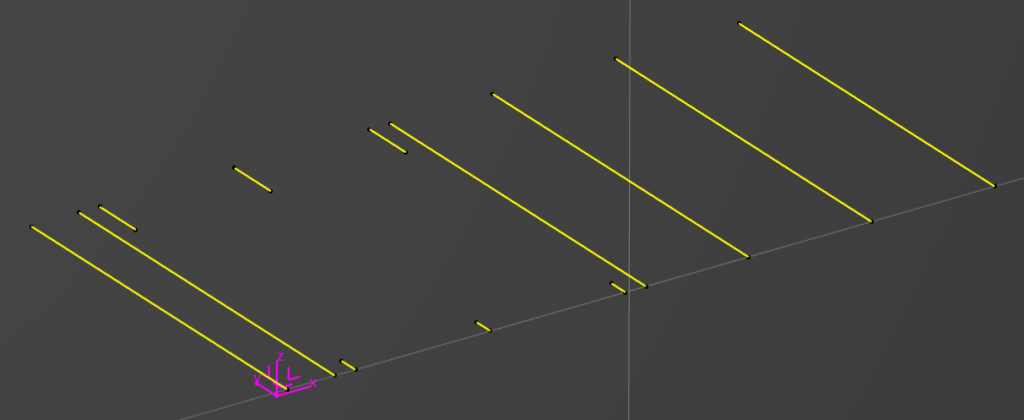
So the problem is we have a series of lines and a reference AxisSystem, we want to sort these from left to right and bottom to top, in respect to the AxisSystem. The problem is some of the lines are colinear, and we want to ensure that the solution can handle multiple colinear lines.

We know that the Z Axis will always be perpendicular to the plane that the lines exist on. So how do we do this.

Setting Up the Action

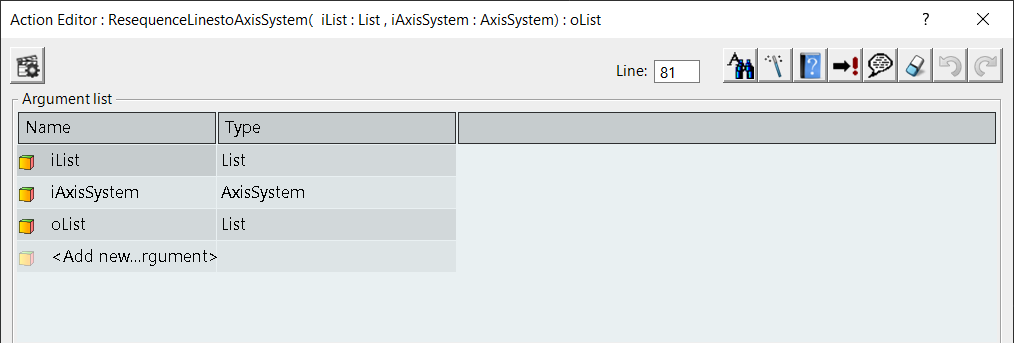
To do this we will cerate an Action, that has two inputs and one output. These will be an Input List of lines to sequence, the reference AxisSystem and an Output List of Lines.

Action Body

Header Comments

The first thing which is best practice is to create a comments section for the inputs and outputs and what the Actions name will be, this will help future development.

/* Action created by me 1/6/2021 */

// iList : List
// iAxisSystem : AxisSystem
// oList : List

// SortLinestoAxisSystem(  iList : List , iAxisSystem : AxisSystem) : oList

Create the AxisSystem Origin Point

We need to retrieve the origin of the AxisSystem to do this we will create 12 real variables and pass them into the GetDirectionOfAxis method which is a function belonging to the AxisSystem this will update these variables into four groups; Three variables for the Axis Origin, Three variables for the X Axis vector, Three variables for the Y Axis vector and Three variables for the Z Axis vector.

We can then create our own point from the Three variables for the Axis Origin, but they have to be converted from Real to Length by multiplying by 1mm.

// Get AxisSystem Origin

Let ioXO , ioYO , ioZO , ioIX , ioIY , ioIZ , ioJX , ioJY , ioJZ , ioKX , ioKY , ioKZ ( Real )
iAxisSystem->GetDirectionOfAxis(ioXO , ioYO , ioZO , ioIX , ioIY , ioIZ , ioJX , ioJY , ioJZ , ioKX , ioKY , ioKZ)

Let ioAxisSystemOrigin ( Point )
ioAxisSystemOrigin = point( ioXO * 1mm , ioYO * 1mm , ioZO * 1mm)

Create the Base Geometry

In the next section of code we’ll create three planes, one that is coplanar to the lines in the list, one that is perpendicular to the lines in the list and a final plane that is perpendicular to the first two planes.

Let ioRefLine1 , ioRefLine2 ( Line )
ioRefLine1 = iList[ 1 ]
ioRefLine2 = iList[ iList->Size() ]

Let ioBasePlane , ioRefPlane1 , ioRefPlane2 ( Plane )
ioBasePlane = plane( centerofgravity( ioRefLine1 ) , ioRefLine2 )

Let ioDirectionLine ( Line )
ioDirectionLine = lineangle( ioRefLine1 , ioBasePlane , ioAxisSystemOrigin , True , 0mm , 1000mm , 90deg , True)

ioRefPlane1 = planenormal( ioDirectionLine , ioAxisSystemOrigin )
ioRefPlane2 = planenormal( ioRefLine1 , ioAxisSystemOrigin )

Initial Grouping Sort

The next section allows us to group the elements in the list by a distance defined from the center point of a line to the reference plane that is parallel to the lines and perpendicular to the plane that is coplanar to the lines, this will naturally sub-group the coplanar lines. This is achieved by adding two length parameters to each line with a rounded distance from the lines center point back to the two reference planes (the second length parameter will be used later). Once we loop through each line adding the two length parameters and setting their values, we can sort the list into new list where the length measurement is increasing i.e. the list will start with the closest line to the AxisSystem and the last line will be the line that is furthest from the AxisSystem.

Note: – There is a bug in the CAD system, when comparing length parameters that are not whole numbers. To avoid this bug in the second sort operation, the initial distance values are rounded to 0 decimal places.

Let ioIndex ( Integer )
ioIndex = 1

Let ioLine ( Line )
For ioIndex While ioIndex<= iList->Size()
{
	Let ioCurrentValue, ioInlineValue ( Length )
	
	ioLine = iList[ ioIndex ]		
	ioCurrentValue = round(distance( ioRefPlane1 , centerofgravity( ioLine )) , "mm" , 3 )
	ioInlineValue = round(distance( ioRefPlane2 , centerofgravity( ioLine )) , "mm" , 3 )
			
	ioLine->SetAttributeDimension( "RefPosition" , ioCurrentValue , "LENGTH" )
	ioLine->SetAttributeDimension( "RefInLine" , ioInlineValue , "LENGTH" )
}

Let ioInitalSort ( List )
ioInitalSort= iList ->Sort( "<" , "Line" , "Length" , "y=x->GetAttributeReal(\"RefPosition\")" )

Final Sort

In the last section we will loop through the lines looking for Sub-Groups, if a Sub-Group is found then the Sub-Group is sorted again using the second length parameter. Then the newly sorted Sub-Group is added to the output list, when there is a Sub-Group, the looping index is incremented by the number of elements in the Sub-Group. If there is no Sub-Group just a single line found, just the single line is added to the output list, and the index incremented by one (done naturally by the For While loop).

ioIndex = 1
oList->RemoveAll()
For ioIndex While ioIndex<= ioInitalSort->Size()
{
	ioLine = ioInitalSort[ ioIndex ]
	
	Let ioRefPositionValue ( Length )
	ioRefPositionValue = ioLine->GetAttributeReal("RefPosition")*1000mm
	
	Let ioInLineList ( List )
	Let ioQueryString ( String )
	ioQueryString = "x->GetAttributeReal(\"RefPosition\") ==" + ioRefPositionValue + ""
	
	ioInLineList = ioInitalSort->Filter("Line", ioQueryString)
	
	if( ioInLineList->Size() == 1)
	{
		oList = oList + ioInLineList
	}
	Else
	{
		Let ioSequencedSubList ( List )
		ioSequencedSubList = ioInLineList->Sort( "<" , "Line" , "Length" , "y=x->GetAttributeReal(\"RefInLine\")" )
		oList = oList + ioSequencedSubList
	}
	
	ioIndex = ioIndex + ioInLineList->Size()
}