Adding Center of Gravity’s
Let’s Start off with a 2D problem, we need to know the current areas of both shapes and the current CoG’s for both shapes:
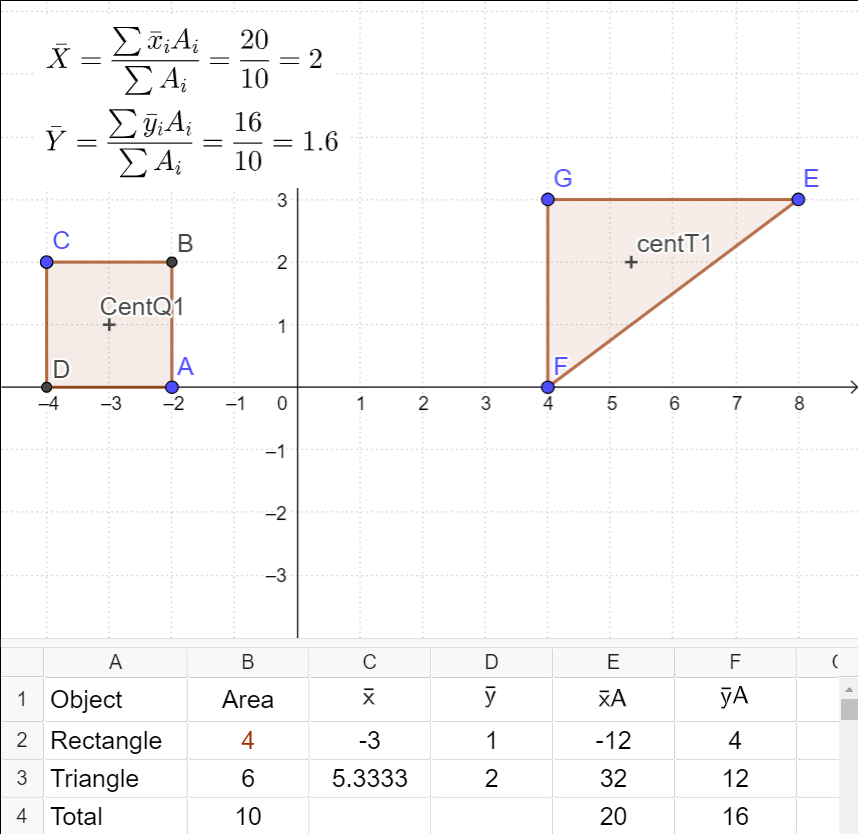
We can then do some basic easy math to figure out the combined CoG:
\bold{Step1} \\
Total Area = 4 + 6 = 10 \\
\bold{Step2} \\
Rectangle \space R\space \overline{x}A = 4 * -3 = -12 \\
Triangle \space T\space \overline{x}A = 6 * 5.3333 = 32 \\
R\space \overline{x}A + T\space \overline{x}A = 20 \\
\bold{Step3} \\
Rectangle \space R\space \overline{y}A = 4 * 1 = 4 \\
Triangle \space T\space \overline{y}A = 6 * 2 = 12 \\
R\space \overline{y}A + T\space \overline{y}A = 16 \\
\bold{Step4} \\
\overline{X} = (20/10) = 2 \\
\overline{Y} = (16/10) = 1.6 \\
To summarize, sum (X . Area) and then divided by the sum of the areas, repeat for Y and Z. This equation can be modified for each magnitude, replace Area with Volume, or Mass.
Volume CoG Addition
So let’s assume that the same problem has symmetrical thickness of +1 -1, we need to calculate one more dimension:
\begin{aligned}
\overline{X} =\dfrac{\sum\overline{x}iAi}{\sum Ai} \\
&
\overline{Y} =\dfrac{\sum\overline{y}iAi}{\sum Ai} \\
&&
\bold{\overline{Z} =\dfrac{\sum\overline{z}iAi}{\sum Ai}} \\
\end{aligned}| Object | Area | Volume | x | y | z | xV | yV | zV |
| Rectangle | 4 | 8 | -3 | 1 | 0 | -24 | 8 | 0 |
| Triangle | 6 | 12 | 5.3333 | 2 | 0 | 63.9996 | 24 | 0 |
| Total | 10 | 20 | 39.9996 | 32 | 0 |
So we simply change Area(A) to Volume(V)
\begin{aligned}
\overline{X} =\dfrac{\sum\overline{x}iVi}{\sum Vi} \\
&
\overline{Y} =\dfrac{\sum\overline{y}iVi}{\sum Vi} \\
&&
\overline{Z} =\dfrac{\sum\overline{z}iVi}{\sum Vi} \\
\end{aligned}In this case since the third dimension is parallel we know that its value will be 0, but lets carry on and see:
\bold{Step1} \\
Total Volume = 8 + 12 = 20 \\
\bold{Step2} \\
Rectangle \space R\space \overline{x}V = 8 * -3 = -24 \\
Triangle \space T\space \overline{x}V = 12 * 5.3333 = 63.9996 \\
R\space \overline{x}V + T\space \overline{x}V = 39.9996 \\
\bold{Step3} \\
Rectangle \space R\space \overline{y}V = 8 * 1 = 8 \\
Triangle \space T\space \overline{y}V = 12 * 2 = 24 \\
R\space \overline{y}V + T\space \overline{y}V = 32 \\
\bold{Step4} \\
Rectangle \space R\space \overline{z}V = 8 * 0 = 0 \\
Triangle \space T\space \overline{z}V = 12 * 0 = 0 \\
R\space \overline{z}V + T\space \overline{z}V = 0 \\
\bold{Step5} \\
\overline{X} = (39.9996/20) = 2 \\
\overline{Y} = (32/20) = 1.6 \\
\overline{Z} = (0/20) = 0 \\
So we were right the third dimension is 0, and the CoG has not changed from the 2D problem, because we added material symmetrically about the mid plane.
Mass CoG Addition
So let’s repeat this time for Mass
| Object | Area | Volume | Density | Mass | x | y | z | xM | yM | zM |
| Rectangle | 4 | 8 | 2 | 16 | -3 | 1 | 0 | -48 | 16 | 0 |
| Triangle | 6 | 12 | 2 | 24 | 5.3333 | 2 | 0 | 127.9992 | 48 | 0 |
| Total | 10 | 20 | 40 | 79.9992 | 64 | 0 |
So we simply change Volume(V) to Mass(M)
\begin{aligned}
\overline{X} =\dfrac{\sum\overline{x}iMi}{\sum Mi} \\
&
\overline{Y} =\dfrac{\sum\overline{y}iMi}{\sum Mi} \\
&&
\overline{Z} =\dfrac{\sum\overline{z}iMi}{\sum Mi} \\
\end{aligned}We perform the exact same math again:
\bold{Step1} \\
Total Mass = 16 + 24 = 40 \\
\bold{Step2} \\
Rectangle \space R\space \overline{x}V = 16 * -3 = -48 \\
Triangle \space T\space \overline{x}V = 24 * 5.3333 = 127.9992 \\
R\space \overline{x}V + T\space \overline{x}V = 79.9996 \\
\bold{Step3} \\
Rectangle \space R\space \overline{y}V = 16 * 1 = 16\\
Triangle \space T\space \overline{y}V = 24 * 2 = 48 \\
R\space \overline{y}V + T\space \overline{y}V = 64 \\
\bold{Step4} \\
Rectangle \space R\space \overline{z}V = 16 * 0 = 0 \\
Triangle \space T\space \overline{z}V = 24 * 0 = 0 \\
R\space \overline{z}V + T\space \overline{z}V = 0 \\
\bold{Step5} \\
\overline{X} = (79.9996/40) = 2 \\
\overline{Y} = (64/40) = 1.6 \\
\overline{Z} = (0/40) = 0 \\Pretty simple right, we know how to handle uniform shapes, with uniform density, lets try something non-uniform.
Let’s assume the Rectangle has a thickness 8 where is midplane is at +4 with a density of 5 and the triangle has a thickness of 3 where it’s midplane is at -6 with a density of 15:
| Object | Area | Volume | Density | Mass | x | y | z | xM | yM | zM |
| Rectangle | 4 | 32 | 5 | 160 | -3 | 1 | 4 | -480 | 160 | 640 |
| Triangle | 6 | 18 | 15 | 270 | 5.3333 | 2 | -6 | 1,439.991 | 540 | -1,620 |
| Total | 430 | 959.991 | 700 | -980 |
Since we have all the information in the table lets just do the last step:
\overline{X} = (959.991/430) = 2.2325 \\
\overline{Y} = (700/430) = 1.6279 \\
\overline{Z} = (-980/430) = -2.2790 \\You can download an excel spreadsheet here with the proof.
