Vectors

Vectors

Vectors, Magnitude and Unit Vectors

A vector is simply a line from point to point, the length of the line is unitless so its not defined by mm, m or inches. If the length of the line is 1 unit, it is a unit vector, or it has a magnitude (line length) of 1 unit. If the length of the line is not 1 unit it is not a unit vector and has a magnitude greater than or less than 1 unit.

If we have 2 points A(100,100,100) and B(200,200,200) we can define a vector AB

\overrightarrow{AB} \\
= Bx - Ax ; By - Ay ; Bz - Az \\
= 200 - 100 ; 200 - 100 ; 200 - 100 \\
\overrightarrow{AB}= 100 ; 100 ; 100 \\
I = 100 ; J = 100 ; K = 100

All that has happened is that the line has been moved, so that it starts at 0,0,0 and its end point is at 100,100,100.

The magnitude of the vector is defined by calculating the length of the line

||{AB}|| \\
= \sqrt{I^2 + J^2 + K^2}  \\
= \sqrt{100^2 + 100^2 + 100^2}  \\
= \sqrt{10,000 + 10,000 +10,000}  \\
= \sqrt{30,000}  \\
||{AB}||= 173.205  \\

The unit vector can be calculated by dividing the vectors components by the magnitude

\widehat{AB} \\
= \overrightarrow{AB} / ||{AB}|| \\
= 100 / 173.205 ; 100 / 173.205 ; 100 / 173.205 ; \\
= 0.577 ; 0.577 ; 0.577 \\
\hat{I} = 0.577 ;  \hat{J} = 0.577 ; \hat{K} = 0.577

Dot Product (Scalar)(Communitive) and Cross Product (Vector)

There are two ways in which vectors can be multiplied together well start with the Dot Product of Vectors AB = 0 ; 4 ; 5 and Vector XY = 0 ; 7 ; 2

\overrightarrow{AB} \cdotp \overrightarrow{XY} \\
= (AB\tiny{X} \normalsize XY\tiny{X} \normalsize)+(AB\tiny{Y} \normalsize XY\tiny{Y} \normalsize)+(AB\tiny{Z} \normalsize XY\tiny{Z} \normalsize)\\
= ( 0 * 0 ) + ( 4 * 7 ) + ( 5 * 2 ) \\
= 0 + 28 + 10 \\
= 38

The Dot Product as a Projection

If we divide the Dot Product scalar value by the magnitude of Vector XY we will get the projection of Vector AB onto Vector XY.

= 38 / ||{XY}|| \\
= \sqrt{I^2 + J^2 + K^2}  \\
= \sqrt{0^2 + 7^2 + 2^2}  \\
= \sqrt{0 + 49 +4}  \\
= \sqrt{53}  \\
||{AB}||= 7.2801  \\
38 / 7.2801 = 5.22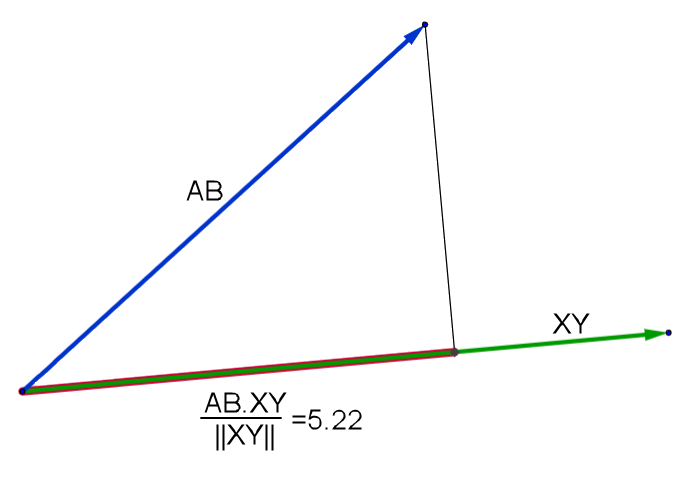

However, we need to look at the this equation in its entirety, for it to be meaningful.

\overrightarrow{AB} \cdotp \overrightarrow{XY} = |\overrightarrow{AB}| \cdotp |\overrightarrow{XY}| Cos\varTheta\\

Cross Product

The cross product of two vectors defines a vector that is perpendicular to both the ordinal vectors.

Lets take Vector(M) = 3 ; 1 ; 4 and Vector(N) = −2 ; 0 ; 5. To find the Cross Product, we form a determinant the first row of which is a unit vector, the second row is our first vector, and the third row is our second vector:

\begin{bmatrix}
   i & j & k \\
   3 & 1 & 4 \\
-2 & 0 & -5
\end{bmatrix}

Now, just expand along the first row:

\begin{bmatrix}
i & j & k \\
3 & 1 & 4 \\
-2 & 0 & 5
\end{bmatrix} =
\begin{bmatrix}
1 & 4 \\
0 & 5
\end{bmatrix} i-
\begin{bmatrix}
3 & 4 \\
-2 & 5
\end{bmatrix} j-
\begin{bmatrix}
3 & 1 \\
-2 & 0
\end{bmatrix} k \\
=(1⋅(5)−(0)⋅(4))i−(3⋅(5)−(−2)⋅(4))j+(3⋅(0)−(−2)⋅(1))k \\
=(5-4)i-(15+8)j+0+2)k \\
=5i−23j+2k \\
=5 ; 23 ; 2

You can download an excel spreadsheet here with the proof.