Table of Contents
Resolving Non-uniform Distributed Loads On a Beam
So far we have covered Point Loads and Distributed Loads on a Beam, we now need to look at Non-Uniform distributed loads.
1 Tonnes in Kips = 2.2046
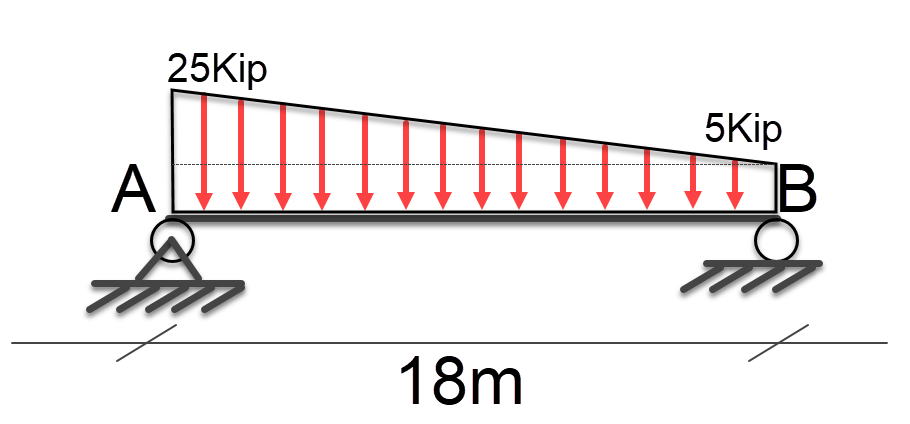
Free Body Diagram
Initially we will simplify this case and assume that the two loads are 20Kip and 0Kip creating a true triangle. Now it’s easy to convert to a point load this is achieved by multiplying (( 20kip * 18 ) / 2 ), the area of a triangle, which equals a point load of 180kip. However where is the point load, well there is a general rule of thirds that can be applied to determine the centroid of a triangle. So in this case we can say that the point load is at 18 / 3 = 6m.
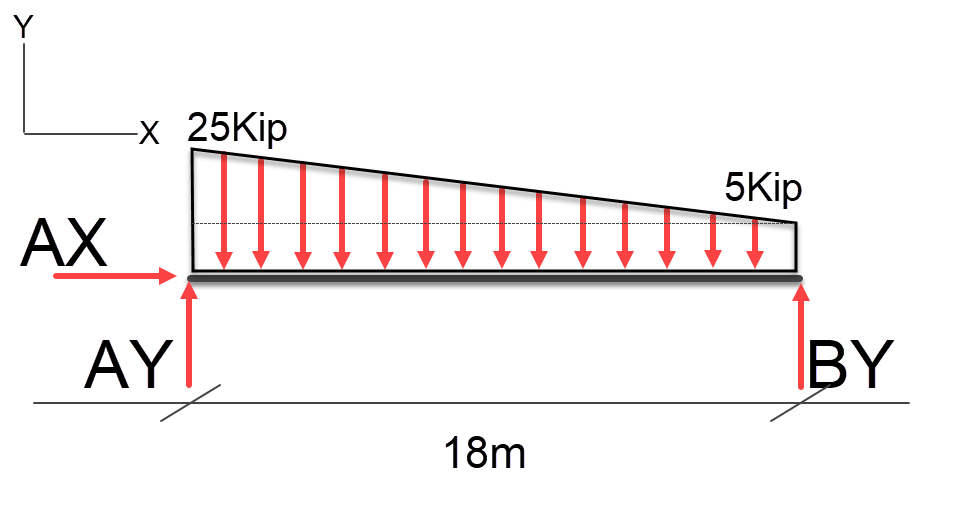
Based on this we can calculate the resulting loads at AY and BY;
Load * Span / TotalSpan \\ AY = (180 * 6 ) / 18 \\ AY = 1080 / 18 \\ AY = 60 \\ BY = (180 * 12 ) / 18 \\ BY = 2160 / 18 \\ BY = 120 \\ Load = 60kip + 120kip = 180kip
However we have to take into account the remaining load the rectangular area. We know this area is (5Kip * 18) = 90Kip point load symmetrical, so we can add 45kip to each side. this results in a solution AY = 105Kip and BY = 165Kip.
Offset Non-uniform Distributed Loads On a Beam
In this case we have a non uniform load that is offset to the side. Using the same process we will break the non-uniform load into two loads a uniform load and a non-uniform triangular load.
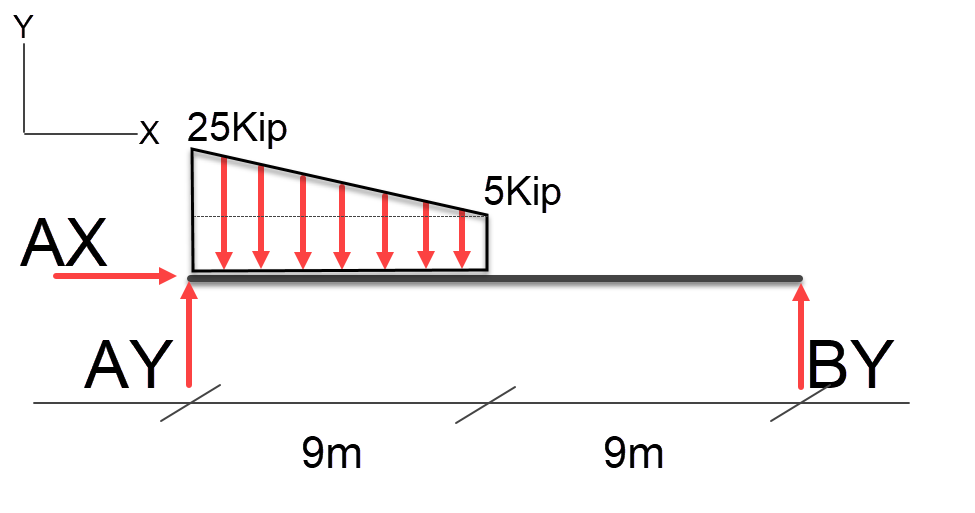
Let’s start off with the non-uniform portion of the load using the thirds rule. (( 20kip * 9 ) / 2 ), the area of a triangle, which equals a point load of 90kip. Again we know that the centroid is 1/3 from the end of the triangle, or 3m.
Load * Span / TotalSpan \\ AY = (90 * 3 ) / 18 \\ AY = 270 / 18 \\ AY = 15 \\ BY = (90 * 15 ) / 18 \\ BY = 1350 / 18 \\ BY = 75 \\ Load = 15kip + 75kip = 90kip
Now we have to calculate the rectangular portion of the nonuniform distributed load, we know this area is (5Kip * 9) = 45Kip point load at 4.5m from the end.
Load * Span / TotalSpan \\ AY = (45 * 4.5 ) / 18 \\ AY = 202.5 / 18 \\ AY = 11.25 \\ BY = (45 * 13.5 ) / 18 \\ BY = 607.5 / 18 \\ BY = 33.75 \\ Load = 11.25kip + 33.75kip = 45kip
Now we know the loads at either end we can now add them together. AY = (15 + 11.25) = 26.25kip and BY = (75 + 33.75) = 108.75kip so as a final check lets make sure that the sum of the point loads equals the sum of the resultants: (90 + 45 ) = ( 26.25 + 108.75) 135 = 135 so its correct.
No if we follow this process we can resolve any complex problem.
Complex Problem
Here is a more complex problem, lets walk through it to resolve the loads for each end. we can quickly do the math on each non uniform load to determine what each one is and the sum total so we can validate our answer. Left-hand load = (((20*9)/2) +( 9*5)) = 135. and Right-hand load = (((40*4.5)/2)+(5*4.5)) = 112.5, the total load is (135 + 112.5) = 247.5kip. Well use this to ensure a correct answer at the end.
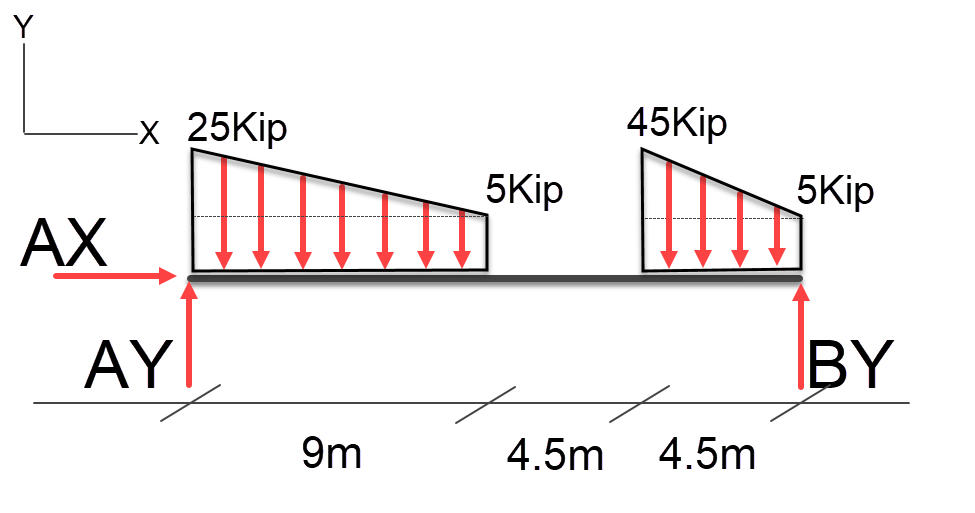
Lets do the left-hand non-uniform load first, in this case I’m going to calculate the both areas at once the rectangle and the triangle.
Load * Span / TotalSpan \\ AY = ((((20*9)/2) * 3 ) / 18 ) + ((5*9) * 4.5) /18 \\ AY = (270 / 18) + (202.5 / 18) \\ AY = 15 + 11.25 \\ AY = 26.25 \\ BY = ((((20*9)/2) * 15 ) / 18 ) + ((5*9) * 13.5) /18 \\ BY = (90 / 18) +(354.375 / 18) \\ BY = 75 + 33.75 \\ BY = 108.75 \\ Load = 26.25kip + 108.75kip = 135kip
Now the right-hand non-uniform load;
Load * Span / TotalSpan \\ AY = ((((40*4.5)/2) * 15 ) / 18 ) + (((5*4.5) * 15.75) /18)\\ AY = (1350 / 18) + (354.375 / 18) \\ AY = 75 + 19.6875 \\ AY = 94.6875 \\ BY = ((((40*4.5)/2) * 3 ) / 18 ) + ((5*4.5) * 2.25) /18\\ BY = (270 / 18) +(50.625 / 18) \\ BY = 15 + 2.8125 \\ BY = 17.8125 \\ Load = 94.6875kip + 20.625kip = 112.5kip
Finally we can add the resultant loads together AY + BY = 247.5kip = 135kip + 112.5kip = 247.5kip
