Table of Contents
Resolving Distributed Loads on a Beam
In a previous post we looked at resolving point loads on a beam in this post we will look at distributed loads.
In this example we will see how to resolve the resultant loads at A and B due to a 12Kips/Meter distributed load.
1 Tonnes in Kips = 2.2046
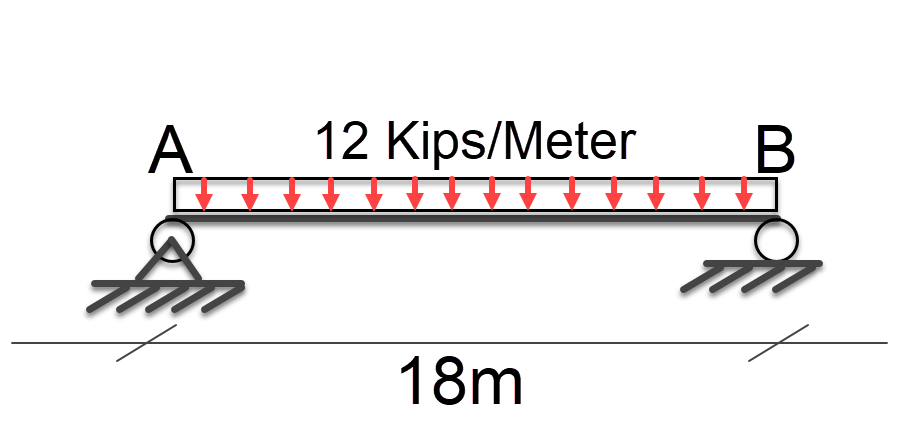
Free Body Diagram
First we will create a free body diagram, to represent our problem.
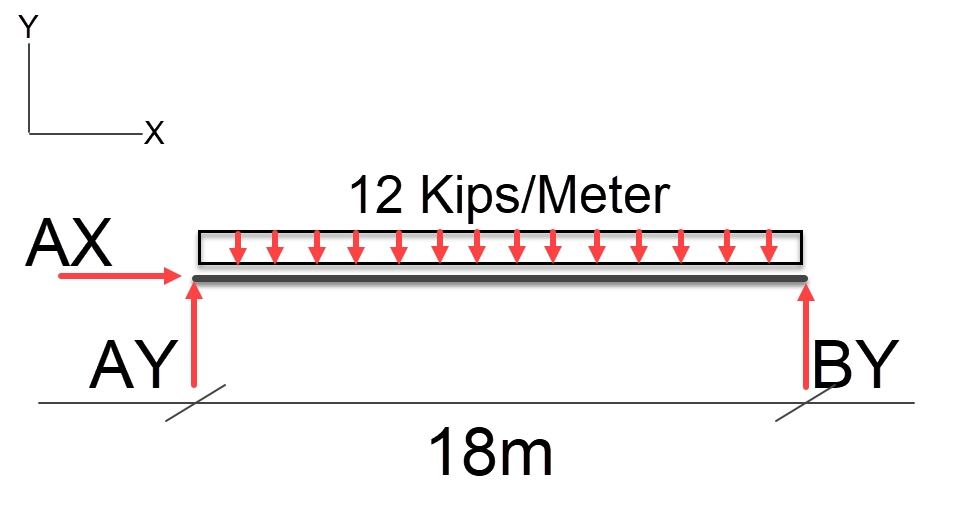
Converting a Uniform Distributed Load to a Point Load
It’s important to note that the AX load is 0kips in this case since no loads have any horizontal component.
In the case of a distributed load, we can convert the distributed load to a point load this is achieved by multiplying distributed load by the distance it’s applied across. Then positioning the point load at the midpoint of the uniform distributed load (as long as its truly uniform).
In our example we have an 18meter span with 12 kips / meter = 18 * 12 = 216kip point load at the mid point of the span.
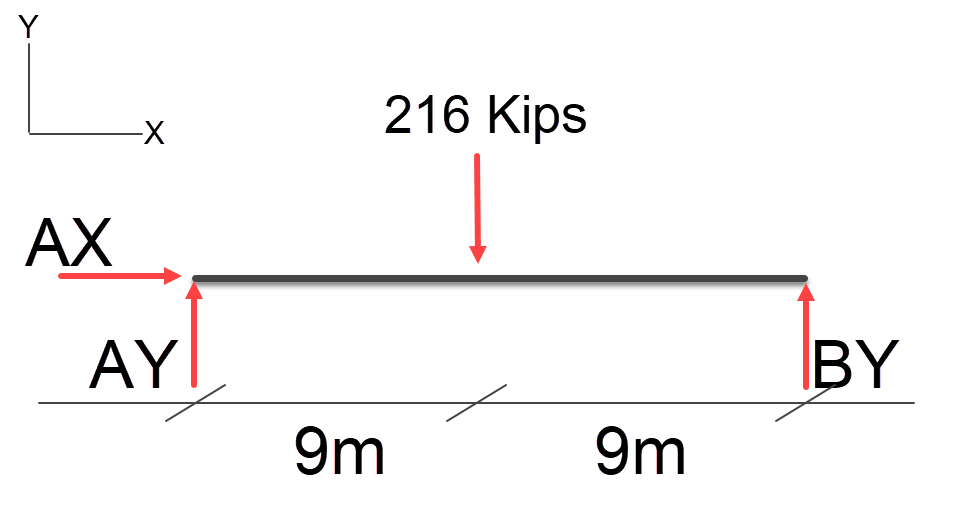
Since its at the mid point of the span we can simply divide this by 2 to find the resultant loads at AY and BY = 108Kips.
Offset Uniform Distributed Load
In this case the distributed load is offset to one side lets look at how we resolve this.
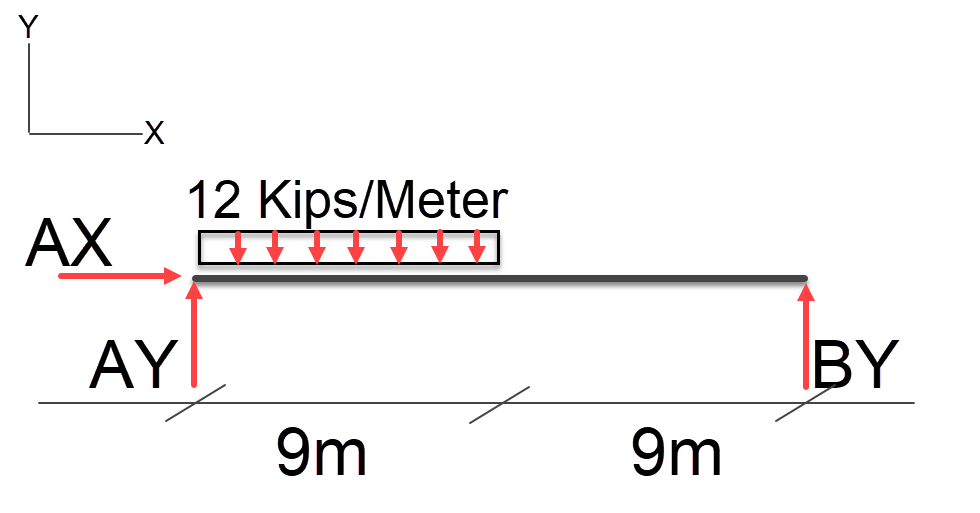
Using the same logic previously applied to convert a uniform distributed load, we can do the same for this example, first we multiple the uniform distributed load by its span 12kips * 9 = 108kip point load at the mid point of the distributed load this is shown below;
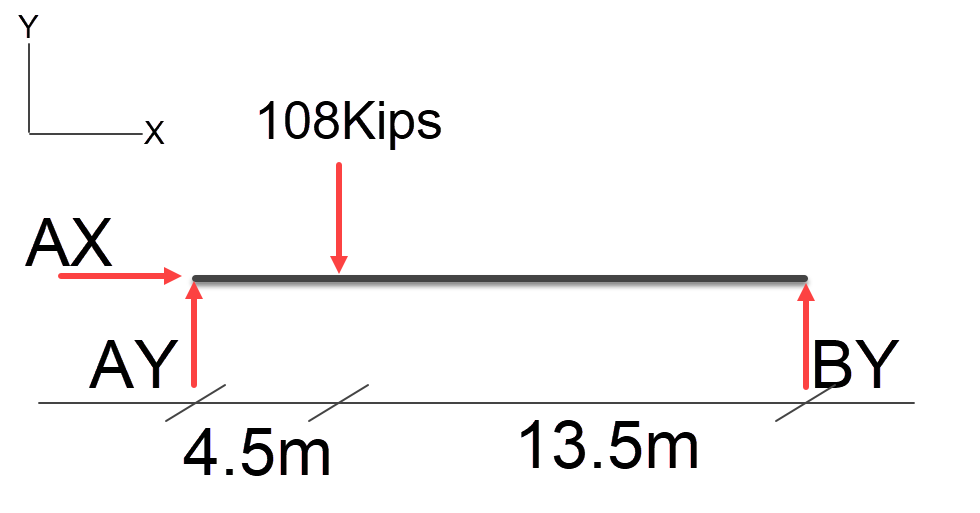
We can now resolve the resultant forces at AY and BY using the point load method.
1 / ( 4.5 + 13.5 ) = 0.0555555 \\ 0.0555555 * 4.5 = 0.25 \\ 108kips * 0.2 = 27kips \\
And we know that BY = Total Point Load – AY, so BY = 81Kips.
We can also do the calculation by;
Load * Span / TotalSpan \\ AY = (108 * 4.5 ) / 18 \\ AY = 486 / 18 \\ AY = 27 \\ BY = (108 * 13.5 ) / 18 \\ BY = 1,458 / 18 \\ BY = 81 \\ Load = 27 + 81 = 108
Multiple Offset Loads
In this case we have two uniform distributed loads lets see how we handle this;
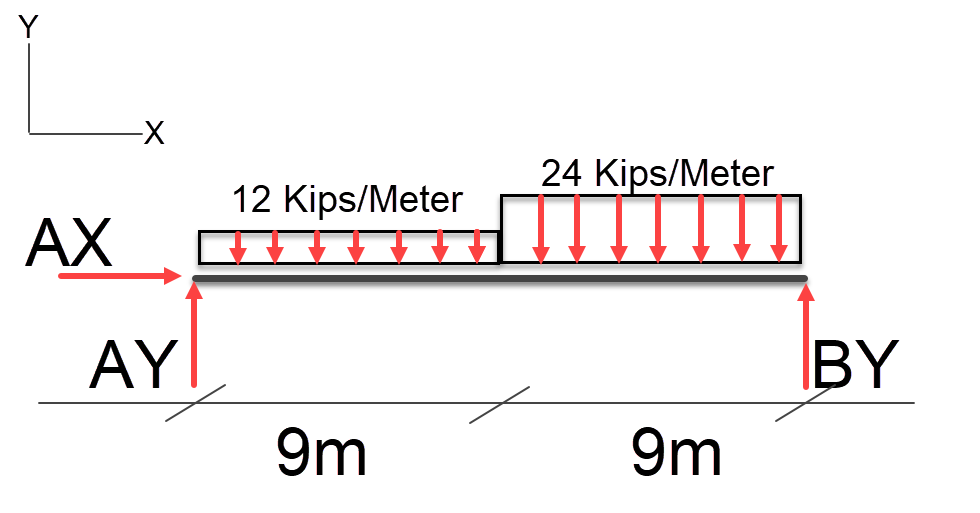
Just as before we convert the uniform distributed loads to point loads;
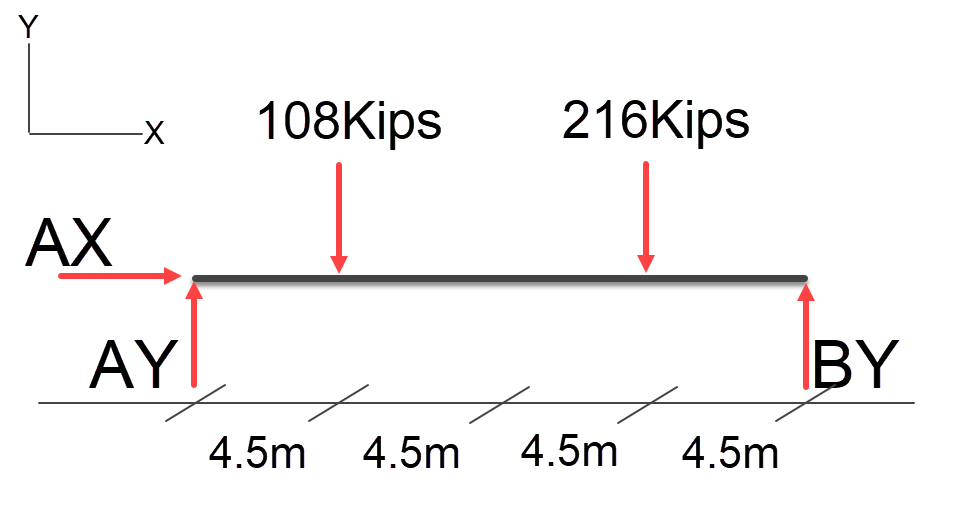
Now we can do the calculations, lets start of with AY;
Load * Span / TotalSpan \\ AY1 = (108 * 4.5 ) / 18 \\ AY1 = 486 / 18 \\ AY1 = 27 \\ AY2 = (216 * 13.5 ) / 18 \\ AY2 = 2916 / 18 \\ AY2 = 162 \\ AY1 + AY2 = 189kips
Next BY;
Load * Span / TotalSpan \\ BY1 = (108 * 13.5 ) / 18 \\ BY1 = 1458 / 18 \\ BY1 = 81 \\ BY2 = (216 * 4.5 ) / 18 \\ BY2 = 972 / 18 \\ BY2 = 54 \\ BY1 + BY2 = 135kips
And as a final check 189 + 135 = 324kips
And as they say that is that, next post will cover Non-Uniform Distributed Loads.
